Barlicity is a modular work that can be presented in three different configurations, under the following names:

1. Barless for piano and detuned sine waves

2. City for stereo fixed media

3. Barlicity for piano and fixed media

You can take a look at the score here. Or you could just check out the score-following video that I made:

Barless is essentially a solo piano work, but one in which the perceived tuning of the piano is modified through a backdrop of detuned sine waves. Through their interference with the notes being played, these sine waves bend certain pitches a little up or down in a calculated way. The result is a kind of just intonation. An interesting side effect of this process is the beating and timbral inflection of the affected notes. (For example, an A played at 440 Hz, when combined with a sine wave at 432 Hz produces a resultant frequency of 436 Hz with a beating at 8 Hz.)

City is a stereo, fixed-media work. It started out as an accompaniment to Barless, consisting of fast, scalar runs on a General MIDI harpsichord, runs which were designed to complement the rhythmic motion of the piano. Ultimately, I decided to send this MIDI data into the CREATE Modular Synthesizer at UCSB and (through many mixes and iterations) turn it into a stand-alone fixed-media piece.

While mixing City, I made a conscious effort to maintain its complementarity with the piano part of Barless. (This was a major challenge, since sometimes what worked well for the tape part on its own did not work well when paired with the piano, or vice-versa.) The end result is that Barless can be combined with City—rather than with the sine wave backdrop—to form a work for piano and fixed media, one which is truly a duet of independent parts. I call this combination Barlicity, in tribute to my former teacher Clarence Barlow.

The three configurations of Barlicity can be presented individually, played sequentially as a three-movement work, or spread throughout a concert program.

The Compositional Process

Barlicity is so named because it resulted from an exploration of several ideas of the composer (and one of my teachers) Clarence Barlow.

The first of these ideas is a rhythmic concept that he terms indispensability. Indispensability is a way of assigning numerical values for the weight of different pulses in a meter. For instance, the six eighth note pulses in a measure of 3/4 have indispensability values of 5, 0, 3, 1, 4, and 2. These numbers indicate that the most important pulse is the downbeat, followed by the third and then the second beat. The offbeats are, of course, less important, and are ordered in accordance with the beat that they lead into. By contrast, the six eighth note pulses in 6/8 have indispensability values of 5, 0, 2, 4, 1, and 3, emphasizing the division of the measure into two main dotted-quarter beats. If not a thousand words, the following picture comparing the 16th-note-level indispensabilities of 3/4, 6/8, and 12/16 from Clarence's book Musiquantics is probably worth at least a couple paragraphs of awkward description:

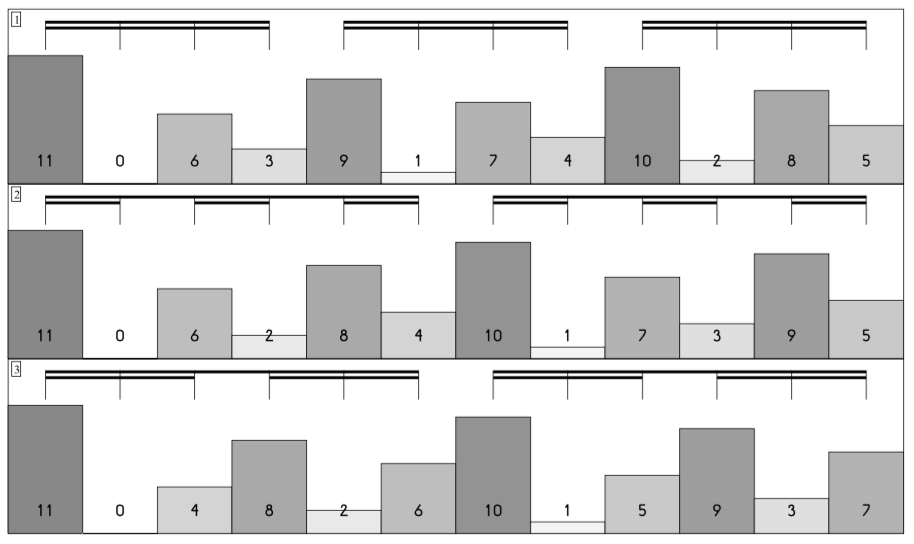
The handiness of having numerical values for pulse importance is that we can use this information in creating algorithmic music. For instance, in the piano part to Barless/Barlicity, I used indispensability to help choose how low or high a pitch is, with lower pitches falling on more significant beats. (This can get a little repetitive, however, so sometimes I inverted the indispensability values to create syncopations.) I also used indispensability in City to determine when running passages should start and stop.

The second concept of Clarence’s that I adopted for this piece is called harmonicity, and is essentially a numerical expression of the stability/consonance of a pitch interval. Any whole-number frequency ratio has an associated harmonicity value that can be calculated from the prime factorization of its numerator and denominator. The smaller the prime numbers involved, the more harmonic the ratio; so for instance, the ratio 9:8 has a far greater harmonicity than the ratio 8:7, because 9, though larger than 7, reduces to 3².

Although harmonicity can only be measured for whole-number frequency ratios, Clarence devised a system for “rationalizing” a set of cent values into a just intoned scale, maximizing the harmonicity between members of the set. For instance, inputting the cent values for a major scale—0, 200, 400, 500, 700, 900, 1100, 1200—we might get the following ratios:

Since harmonicity is a metric describing the harmonic relatedness of two pitches, one of its more evocative applications is to use it in combination with a process called multidimensional scaling to create a map of a given tuning. The following such graph of the 12 tones of a (just-intoned) chromatic scale is again taken from Musiquantics, and you can see that closely harmonically related notes are nearby to one another:

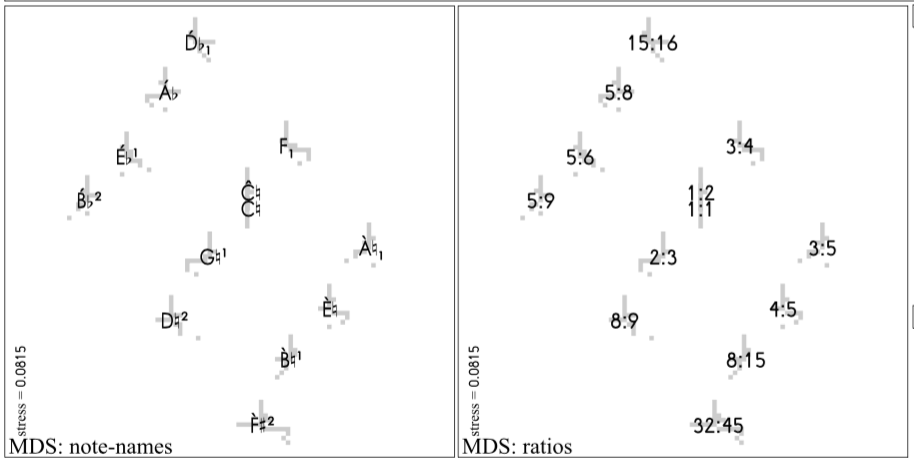
This finally brings us back to Barlicity. In composing the piano part, I re-implemented Clarence’s scale rationalization system in Python and used it to derive a just tuning of the Bark scale. I then used multidimensional scaling to create a map of these pitches, such that more harmonically related pitches are closer together. Finally, I allowed the piano to wander around this space, drawing from different regions over the course of the piece. The following is a screenshot of a visualization that I made (notes the piano is currently playing are in the blue circle):

Many thanks to Clarence for introducing me to these ideas, to Joel Feigin for encouraging me to turn this into a modular work, and to Curtis Roads, Michael Hetrick and CREATE for putting together the CREATE Modular Synthesizer.