Intimate Expanse is a work for String Quartet and that I wrote for the LA-based Formalist Quartet. The "expanse", among other things, refers to the fact that the quartet is situated around the audience, at times enveloping them in sound, and at other times calling to each other as if from across a lake. Despite the distance, there is nevertheless an intimacy to the communication; string quartets are, after all, one of the most intimate performance ensembles.

Here is Formalist Quartet, performing Intimate Expanse at UCSB's Geiringer Hall in February 2018:

For audio only, click here.

You can also check out the score here.

At the heart of this work is a unique scordatura, an Italian term meaning that each player has tuned some of his or her strings a little sharp or flat in a precise manner. The purpose of this is to increase the ability of the musicians to play just intervals, especially with open strings and natural harmonics.

For those uninitiated into the world of just intonation, here is an abbreviated explanation: the standard musical intervals, like the octave, perfect fifth, and major third, correspond to simple ratios in frequency (2/1, 3/2, and 5/4 respectively), with simpler ratios generally corresponding to more consonant intervals. However, these intervals don't fit together perfectly; for instance, if you start at a given note and ascend by three major thirds, you would expect from a piano keyboard to go up by an octave, but the resulting ratio is 5/4 * 5/4 * 5/4 = 125 / 64, which is a little less than the 2/1. This is because instruments like the piano are a compromise: when you play a major third on a piano, it is a little larger than the ideal 3/2 frequency ratio.

A "just" interval is one that sticks to the precise frequency ratio rather than compromising, and it starts to get really interesting when you start playing ratios like 7/4, which is almost exactly halfway between a major 6th and a minor 7th on the piano. This is what my tuning is designed to make possible; by tuning some strings down by a fraction on a half-step, these "just" sevenths, along with the just major thirds, become easy to play.

Once you start including intervals like this, you find yourself in foreign harmonic territory. So being the kind of composer I am, I naturally decided to write a computer program to map out and explore the space of harmonic possibilities. In the following screen capture from the program, each labeled point represents a note played by one of the instruments of the quartet:

This map was made using a process called multidimensional scaling, which allows to you take pair-wise distances between points and turn them into a map. For instance, if you have several cities and you know the distances between every pair of them, you can construct a map from that information using multidimensional scaling.

In this case, the distance between any two notes is based on how complicated the frequency ratio between those notes is, as calculated using Clarence Barlow's formula for harmonicity. (Actually, the whole idea of using multidimensional scaling in the first place was also Clarence's.) What this means is that the notes that are far away from each other are more distantly related harmonically / have a more complicated ratio of frequencies, while the notes that are closer to one another are more closely related and have a simple frequency ratio. Interestingly, there are two main chasms in the map, one resulting from a factor of 5 in the ratio (the just 3rd), and the one from a factor of 7 (the just 7th):

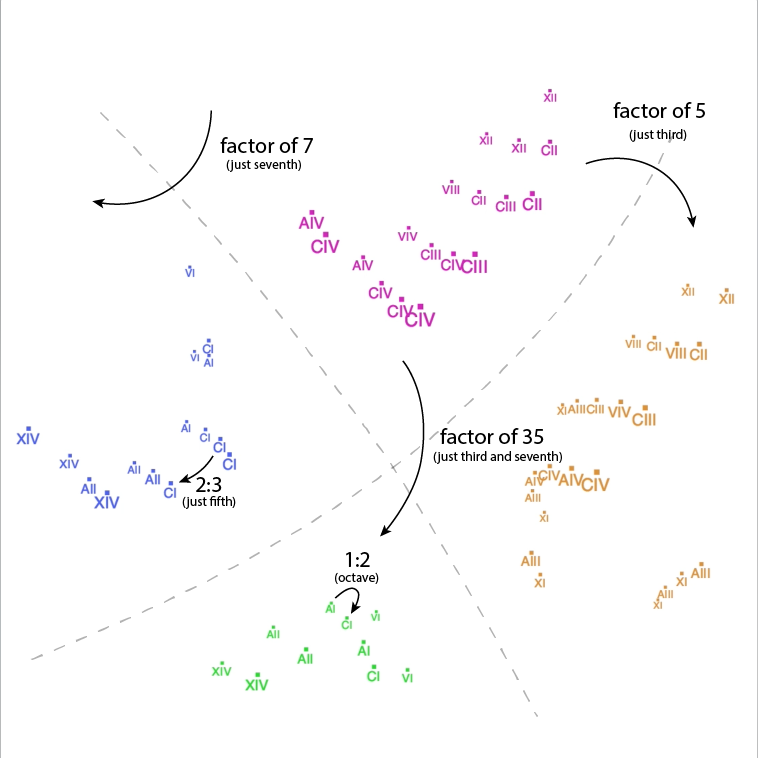
I used my harmony exploration program to assemble interesting chords by ear, and then I connected them in such a way that they formed a circle around the space. From there, I expanded the chords into different sonic textures, and moved between these textures to create a form. The result is a piece driven by the harmonic language of a foreign land, one that I still don't fully understand, but for which I at least had a map.